Next: Άσκηση 8
Up: Άσκηση 7
Previous: Υπόδειξη
Λύση
Είναι:
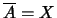 αν και μόνο αν κάθε
αν και μόνο αν κάθε 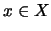 είναι σημείο επαφής του
είναι σημείο επαφής του  ,
δηλαδή αν και μόνο αν για κάθε
,
δηλαδή αν και μόνο αν για κάθε 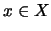 και κάθε
και κάθε
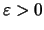 ισχύει
ισχύει
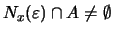 .
Ο
.
Ο 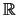 είναι διαχωρίσιμος: παίρνουμε
είναι διαχωρίσιμος: παίρνουμε 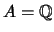 .
Το
.
Το 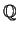 έχει αριθμήσιμο πλήθος στοιχείων και αν
έχει αριθμήσιμο πλήθος στοιχείων και αν
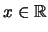 και
και
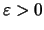 ,
τότε υπάρχουν ρητοί στο
,
τότε υπάρχουν ρητοί στο
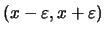 .
Δηλαδή,
.
Δηλαδή,
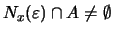 .
)
.
)
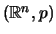 είναι διαχωρίσιμος: παίρνουμε
είναι διαχωρίσιμος: παίρνουμε
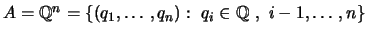 .
Το
.
Το  είναι αριθμήσιμο εαν καρτεσιανό γινόμενο πεπερασμένου πλήθους αριθμησίμων συνόλων. Έστω
είναι αριθμήσιμο εαν καρτεσιανό γινόμενο πεπερασμένου πλήθους αριθμησίμων συνόλων. Έστω
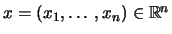 και
και
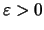 .
Για κάθε
.
Για κάθε
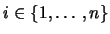 μπορούμε να βρούμε
μπορούμε να βρούμε 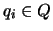 του
του
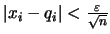 .
Τότε,
.
Τότε,
Δηλαδή,
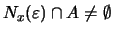 .
Άρα,
.
Άρα,
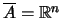 .
.
Άσκηση 7
Υπόδειξη
root
1999-07-29