


Next: Υπόδειξη
Up: Στοιχεία Θεωρίας
Previous: Λύση
Άσκηση 6
Έστω μη κενό υποσύνολο 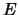 μετρικού χώρου
μετρικού χώρου 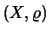 .
Ορίζουμε την απόσταση σημείου
.
Ορίζουμε την απόσταση σημείου 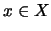 από το
από το 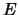 ως εξής:
ως εξής:
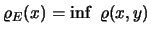 .
(α) Αποδείξτε την ύπαρξη του infimum.
.
(α) Αποδείξτε την ύπαρξη του infimum.
(β) Αποδείξτε ότι:
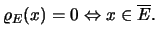
(γ) Αποδείξτε ότι:
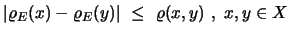 και ότι η
και ότι η
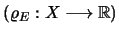 είναι συνεχής στον
είναι συνεχής στον 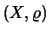 .
Υπόδειξη
Λύση
.
Υπόδειξη
Λύση
root
1999-07-29