


Next: Σειρές πραγματικών αριθμών
Up: Άσκηση 7
Previous: Υπόδειξη
Λύση
Χρησιμοποιούμε απαγωγή στο άτοπο. Υποθέτουμε οτι η 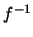 δεν είναι συνεχής
σε κάποιο
δεν είναι συνεχής
σε κάποιο 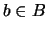 .
Τότε υπάρχουν
.
Τότε υπάρχουν
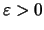 και μία ακολουθία
και μία ακολουθία 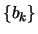 στο
στο 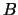 ώστε
ώστε
Θέτουμε
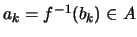 .
Το
.
Το  είναι συμπαγές, άρα υπάρχει υποακολουθία
είναι συμπαγές, άρα υπάρχει υποακολουθία
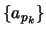 της
της 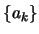 που συγκλίνει σε κάποιο
που συγκλίνει σε κάποιο 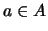 .
Από τη συνέχεια της
.
Από τη συνέχεια της 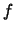 έχουμε
έχουμε
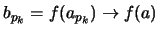 .
Όμως
.
Όμως
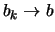 άρα
άρα
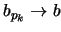 .
Από τη μοναδικότητα του ορίου,
.
Από τη μοναδικότητα του ορίου, 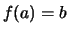 δηλαδή
δηλαδή
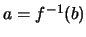 .
.
Έχουμε
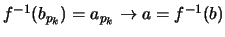 .
Αυτό είναι άτοπο αφού
.
Αυτό είναι άτοπο αφού
για κάθε 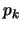 .
.
Άσκηση 7
Υπόδειξη
root
1999-07-29
![]() .
Αυτό είναι άτοπο αφού
.
Αυτό είναι άτοπο αφού