Next: Άσκηση 1
Up: No Title
Previous: Λύση
Ορισμός 21
Αν έχουμε μια ακολουθία
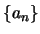
στο
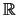
θεωρούμε την ακολουθία
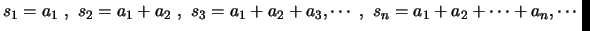
Αν η
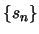
συγκλίνει σε πραγματικό αριθμό
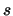
τότε γράφουμε
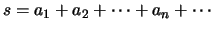
Χρησιμοποιούμε επίσης τις συντομεύσεις:
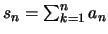
και αν η
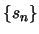
συγκλίνει σε πραγματικό αριθμό
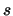
,
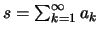
.
Το σύμβολο
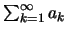
ονομάζεται
σειρά της
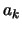
.
Αν μια σειρά συγκλίνει σε πραγματικό αριθμό και απαλείψουμε ένα πεπερασμένο πλήθος όρων της, τότε πάλι θα συγκλίνει σε πραγματικό
αριθμό. Το ίδιο και αν αλλάξουμε ένα πεπερασμένο πλήθος όρων της.
Πρόταση 22
(α) Αν
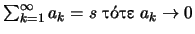
(β) Αν η
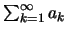
συγκλίνει τότε
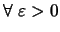
υπάρχει
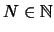
ώστε
Μερικά παραδείγματα:
(α) Η γεωμετρική σειρά
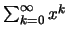 όπου
όπου
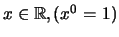 συγκλίνει αν και μόνο αν
συγκλίνει αν και μόνο αν 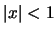 τότε
τότε
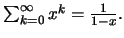
(β) Τηλεσκοπικές σειρές
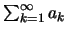 όπου
όπου
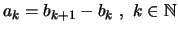 .
Τότε η
.
Τότε η
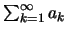 συκλίνει αν και μόνο αν η ακολουθία
συκλίνει αν και μόνο αν η ακολουθία 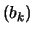 συγκλίνει και μάλιστα ισχύει
συγκλίνει και μάλιστα ισχύει
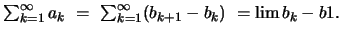
Θεώρημα 23 (Κριτήριο Cauchy)
. Έστω η σειρά
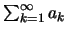
.
Αυτή συγκλίνει αν και μόνο αν ισχύει το εξής:
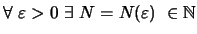
ώστε
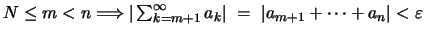
.
Με χρήση του κριτηρίου Cauchy μπορεί να δείξει κανείς ότι η
αρμονική σειρά
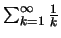
αποκλίνει.
Θεώρημα 24
Έστω η σειρά
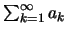
με
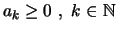
και
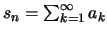
.
Η σειρά συγκλίνει αν και μόνο αν η
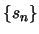
είναι άνω φραγμένη. Αν η
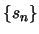
δεν είναι άνω φραγμένη τότε
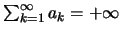
.
Συνέπεια αυτού του θεωρήματος είναι ότι η σειρά
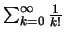
συγκλίνει. Μάλιστα
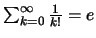
.
Πρόταση 25 (Κριτήριο συμπύκνωσης του Cauchy)
. Αν η σειρά
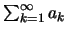
έχει όρους που φθίνουν
προς το μηδέν τότε αυτή συγκλίνει αν και μόνο αν η σειρά
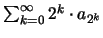
συγκλίνει.
Η πρόταση αυτή εύκολα δίνει ότι η σειρά
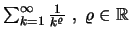
συγκλίνει αν και μόνο αν
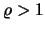
.
Ορισμός 26
Λέμε οτι μια σειρά
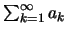
συγκλίνει απολύτως αν η
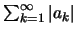
συγκλίνει.
Λέμε οτι συγκλίνει υπό συνθήκη αν συγκλίνει αλλά δεν συγκλίνει απολύτως.
Θεώρημα 27 (Σύγκριση σειρών)
Έστω οι σειρές
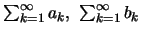
με
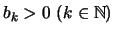
(α) Αν υπάρχει αριθμός 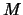 ώστε
ώστε
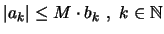 ,
τότε αν η
,
τότε αν η
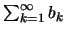 συγκλίνει, θα συγκλίνει
απολύτως η
συγκλίνει, θα συγκλίνει
απολύτως η
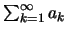 .
.
(β) Αν η
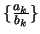 συγκλίνει σε πραγματικό αριθμό, τότε αν η
συγκλίνει σε πραγματικό αριθμό, τότε αν η
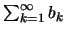 συγκλίνει θα συγκλίνει απολύτως η
συγκλίνει θα συγκλίνει απολύτως η
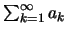 .
.
Θεώρημα 28 (Κριτήριο λόγου D' Alembert)
. Έστω η σειρά
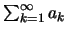
με μη μηδενικούς όρους.
(α) Αν
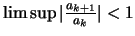 τότε η
τότε η
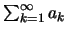 συγκλίνει απολύτως
συγκλίνει απολύτως
(β) Αν
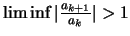 τότε η σειρά
τότε η σειρά
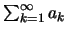 αποκλίνει
αποκλίνει
(γ) Αν
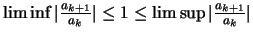 τότε
δεν υπάρχει συμπέρασμα.
τότε
δεν υπάρχει συμπέρασμα.
Θεώρημα 29 (Κριτήριο ρίζας του Cauchy)
. Έστω η σειρά
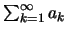
.
(α) Αν
![$\limsup \sqrt [k] {\vert a-k\vert} <1$](img521.gif) τότε η σειρά συγκλίνει απολύτως
τότε η σειρά συγκλίνει απολύτως
(β) Αν
![$\limsup \sqrt [k]{\vert a_k\vert}>1$](img522.gif) τότε η σειρά αποκλίνει
τότε η σειρά αποκλίνει
(γ) Αν
![$\limsup \sqrt [k] {\vert a_k\vert}=1$](img523.gif) τότε δεν υπάρχει συμπέρασμα
τότε δεν υπάρχει συμπέρασμα
Θεώρημα 30 (Dirichlet)
Έστω δυο ακολουθίες
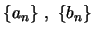
με τις ιδιότητες
(α) Η
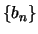
φθίνει προς το μηδέν
(β) Η
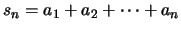
είναι φραγμένη:
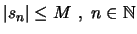
.
Τότε η
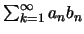
συγκλίνει.
Συνήθως αυτό το θεώρημα χρησιμοποιείται στις
εναλλάσουσες σειρές όπου 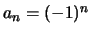 .
.
root
1999-07-29