


Next: Άσκηση 3
Up: Άσκηση 2
Previous: Υπόδειξη
Λύση
(α) Αν 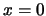 προφανώς συγκλίνει. Αν
προφανώς συγκλίνει. Αν 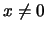 με το κριτήριο του λόγου :
με το κριτήριο του λόγου :
Αν 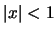 η σειρά συγκλίνει. Αν
η σειρά συγκλίνει. Αν 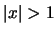 αποκλίνει. Αν
αποκλίνει. Αν 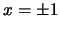 τότε
τότε
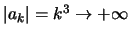 άρα η σειρά αποκλίνει. Δηλαδή η
άρα η σειρά αποκλίνει. Δηλαδή η
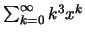 συγκλίνει απολύτως αν
συγκλίνει απολύτως αν 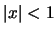 .
.
Με το κριτήριο ρίζας
και συμεχίζουμε όπως πρίν.
(β) Με το κριτήριο της ρίζας:
Άρα η σειρά συγκλίνει όποιο και αν είναι το
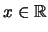 .
.
(γ) Με το κριτήριο της ρίζας:
Αν 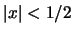 τότε η σειρά συγκλίνει απολύτως. Αν
τότε η σειρά συγκλίνει απολύτως. Αν 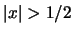 τότε η σειρά
αποκλίνει. Αν
τότε η σειρά
αποκλίνει. Αν 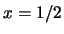 προκύπτει η
προκύπτει η
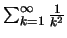 που συγκλίνει,
ενώ αν
που συγκλίνει,
ενώ αν 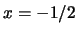 προκύπτει η
προκύπτει η
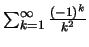 που συγκλίνει
απολύτως.
που συγκλίνει
απολύτως.
Άρα η σειρά
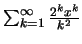 συγκλίνει αν
συγκλίνει αν
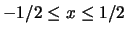 .
Άσκηση 2
Υπόδειξη
.
Άσκηση 2
Υπόδειξη
root
1999-07-29
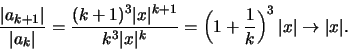
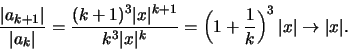
![]() συγκλίνει αν
συγκλίνει αν
![]() .
Άσκηση 2
Υπόδειξη
.
Άσκηση 2
Υπόδειξη