


Next: Άσκηση 45
Up: Άσκηση 44
Previous: Υπόδειξη
Eφόσον το  μπορεί να θεωρηθεί διανυσματικός χώρος πάνω στον
εαυτό του έχουμε ότι dim
μπορεί να θεωρηθεί διανυσματικός χώρος πάνω στον
εαυτό του έχουμε ότι dim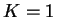 .
Θα δείξουμε ότι dim
.
Θα δείξουμε ότι dim
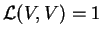 .
Πράγματι, αφού dim
.
Πράγματι, αφού dim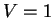 ,
υπάρχει
,
υπάρχει  ώστε το
ώστε το
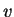 να παράγει τον
να παράγει τον  .
Tότε, αν
.
Tότε, αν  είναι μια μη-μηδενική
γραμμική απεικόνιση τότε κάθε άλλη γραμμική απεικόνιση γράφεται
σαν πολλαπλάσιο της
είναι μια μη-μηδενική
γραμμική απεικόνιση τότε κάθε άλλη γραμμική απεικόνιση γράφεται
σαν πολλαπλάσιο της  .
Πράγματι, αν
.
Πράγματι, αν
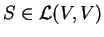 ,
τότε το
,
τότε το
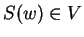 για κάθε
για κάθε 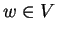 και επειδή
και επειδή  γραμμική και
γραμμική και 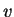 βάση
του
βάση
του  ,
υπάρχει
,
υπάρχει 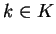 ώστε
ώστε 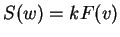 .
Άρα dim
.
Άρα dim
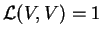 και το αποτέλεσμα προκύπτει από το Πόρισμα 5.
και το αποτέλεσμα προκύπτει από το Πόρισμα 5.
Vassilis Metaftsis
1999-09-15