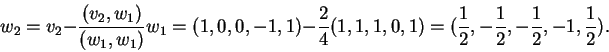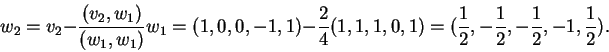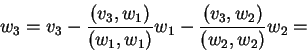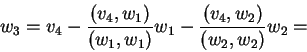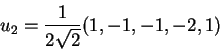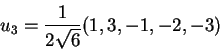Next: Άσκηση 66
Up: Άσκηση 65
Previous: Υπόδειξη
Θέτουμε
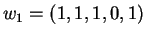 .
Tότε,
.
Tότε,
Για να
απαλαγούμε από τα κλάσματα αντικαθιστούμε το τελευταίο διάνυσμα με
το διπλασιό του και έχουμε
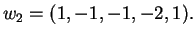
To τελευταίο δείχνει ότι το 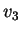 είναι γραμμικώς
συνδυασμός των
είναι γραμμικώς
συνδυασμός των 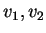 και άρα μπορούμε να το παραλήψουμε.
Επομένως,
και άρα μπορούμε να το παραλήψουμε.
Επομένως,
Προκειμένου να μην έχουμε κλάσματα, αντικαθιστούμε το διάνυσμα
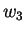 με το
με το
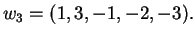 Κανονικοποιώντας την βάση
Κανονικοποιώντας την βάση
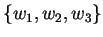 παίρνω
παίρνω
Vassilis Metaftsis
1999-09-15