


Next: Άσκηση 23
Up: Άσκηση 22
Previous: Υπόδειξη
Από την προηγούμενη άσκηση έχουμε ότι
αν και μόνο αν
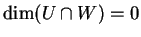 δηλαδή αν
και μόνο αν
δηλαδή αν
και μόνο αν 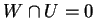 .
.
Γενικότερα, αν το άθροισμα είναι ευθύ τότε με πολλαπλή εφαρμογή του
συμπεράσματος για δύο υπόχωρους παίρνουμε
Αντίστροφα, θα χρησιμοποιήσουμε επαγωγή. Για 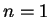 δεν έχουμε
τίποτα να δείξουμε. Υποθέτω ότι ισχύει για
δεν έχουμε
τίποτα να δείξουμε. Υποθέτω ότι ισχύει για 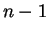 ,
δηλαδή αν
,
δηλαδή αν
τότε το άθροισμα είναι ευθύ. Υποθέτω ότι
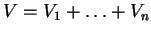 με
με
Tότε από το αποτέλεσμα του πρώτου
μέρους της άσκησης,
To αποτέλεσμα προκύπτει από την υπόθεση της επαγωγής.
Vassilis Metaftsis
1999-09-15
![]() δεν έχουμε
τίποτα να δείξουμε. Υποθέτω ότι ισχύει για
δεν έχουμε
τίποτα να δείξουμε. Υποθέτω ότι ισχύει για ![]() ,
δηλαδή αν
,
δηλαδή αν