ΥΠΟΒΙΒΑΣΜΟΣ ΤΑΞΗΣ ΜΙΑΣ ΟΜΟΓΕΝΟΥΣ ΓΡΑΜΜΙΚΗΣ ΔΙΑΦΟΡΙΚΗΣ ΕΞΙΣΩΣΗΣ
Έστω η ομογενής γραμμική διαφορική εξίσωση τάξης
![]() , (1)
, (1)
όπου οι συντελεστές
Αν
![]() . (2)
. (2)
Αντικαθιστώντας στη συνέχεια τη σχέση (2) στην εξίσωση (1) και χρησιμοποιώντας τον γνωστό κανόνα
![]() ,
,
για
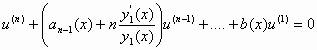 , (3)
, (3)
όπου
![]() , (4)
, (4)
παίρνουμε την
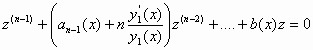 , (5)
, (5)
ως προς
Συμπέρασμα
: Αν είναι γνωστή μια μερική λύσηΣημείωση
: Η παραπάνω μέθοδος υποβιβασμού τάξης για μια ομογενή γραμμική διαφορική εξίσωση οφείλεται στον Γάλλο μαθηματικό D’Alembert (1717-1783).
[
Επιστροφή στα Περιεχόμενα]
ΑΣΚΗΣΕΙΣ
:1. Να λυθεί η διαφορική εξίσωση
![]() ,
, ![]() ,
,
αν ![]() είναι μια ειδική λύση της. [Λύση]
είναι μια ειδική λύση της. [Λύση]
![]() ,
, ![]() ,
,
να βρεθεί μια δεύτερη γραμμικώς ανεξάρτητη λύση. [Λύση]
3. Έστω ότι ![]() και
και ![]() είναι
δοσμένες συνεχείς συναρτήσεις σ’ ένα
ανοικτό διάστημα
είναι
δοσμένες συνεχείς συναρτήσεις σ’ ένα
ανοικτό διάστημα ![]() .
Αν
.
Αν![]() είναι
μια μη-μηδενική λύση της διαφορικής
εξίσωσης
είναι
μια μη-μηδενική λύση της διαφορικής
εξίσωσης
![]() ,
,
να βρεθεί η γενική της λύση. [Λύση]
[Επιστροφή στα Περιεχόμενα]