Λύση

'Εστω $x, y \in [a, b], \; x < y.$ Επειδή η συνάρτηση είναι παραγωγίσιμη στο $[α,β]$ ικανοποιούνται οι προ"υποθέσεις του θεωρήματος της μέσης τιμής στο $[x, y]$ και άρα έχουμε

$$\frac{f(y) - f(x)}{y-x } = f' (\xi), \;\; \xi \in [x,y].$$

Επειδή η παράγωγος είναι φραγμένη, υπάρχει 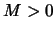$Μ >0$ τέτοιο ώστε $\vert f'(x)\vert < M, \;\; \forall x \in [a,b]$ και άρα

$$\left\vert \frac{f(y) - f(x)}{y-x }\right\vert = \vert f' (\x... ... f(y) - f(x)\vert < M \vert y-x\vert,\;\; \forall x \in [a,b].$$

Στη συνέχεια χρησιμοποιούμε την άσκηση 1.

'Ασκηση 9 Υπόδειξη