'Εστω SRⁿ και xRⁿ. Το x θα λέγεται σημείο συσσώρευσης (σ.σ.) του συνόλου S αν για κάθε ε>0 το σύνολο (Β(x, ε)\{x}) S είναι μη κενό.

Αυτό σημαίνει ότι η μπάλα με κέντρο το x και ακτίνα ε τέμνει το S σε ένα σημείο διαφορετικό από το x. (δεν μας απασχολεί αν το x είναι σημείο του S).

Παράδειγμα: Έστω S = [0, 1){2}. Παρατηρούμε ότι τα 0, 1 είναι σημεία συσσώρευσης του S αλλά το 2 δεν είναι. Άρα ένα σημείο συσσώρευσης του S δεν είναι αναγκαστικά στο S. Όπως θα δούμε παρακάτω, επειδή το 2 δεν είναι σ.σ. του S, δεν θα εξετάσουμε το όριο μίας συνάρτησης f : S® R στο σημείο αυτό.

Ορισμός: Έστω SRⁿ , x σ.σ. του S και f : S® R μια συνάρτηση. Θα λέμε ότι η f έχει στο x οριακή τιμή (ή όριο) αR όταν για κάθε ε>0 υπάρχει δ = δ(ε, x) >0 τέτοιο ώστε |f(y) – a| < ε για κάθε yB(x, δ)S.

(παρατηρούμε ότι B(x, δ)S απο τον ορισμό του σ.σ.)

Ιδιότητες ορίου: Έστω ότι οι f, g έχουν όριο στο x. Τότε

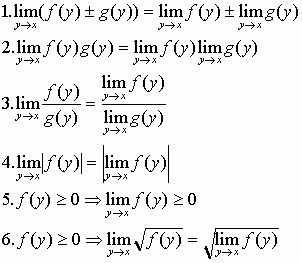
(Στην 3 παραπάνω υποθέτουμε ότι η g είναι μη αρνητική σε μια γειτονιά του x. Στις 5, 6 υποθέτουμε ότι η f είναι μη αρνητική σε μια γειτονιά του x).

Θεώρημα: Η f έχει στο x όριο αR αν και μόνο αν για κάθε ακολουθία {x_n} σημείων του S που συγκλίνει στο x, η ακολουθία f(x_n) συγκλίνει στο α.

Θεώρημα: Αν υπάρχει το όριο

ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ

Ορισμός: : Έστω SRⁿ , xS και f : S® R μια συνάρτηση. Θα λέμε ότι η f είναι συνεχής στο x αν η f έχει στο x όριο f(x), δηλαδή όταν για κάθε ε>0 υπάρχει δ = δ(ε, x) >0 τέτοιο ώστε |f(y) – f(x)| < ε για κάθε yB(x, δ)S.

Θεώρημα: Η f είναι συνεχής στο xS αν και μόνο αν για κάθε ακολουθία {x_n} σημείων του S που συγκλίνει στο x, η ακολουθία f(x_n) συγκλίνει στο f(x).

Θεώρημα: Αν η f είναι συνεχής στο x και η g συνεχής στο f(x) τότε η σύνθεση gf είναι συνεχής στο x.

Θεώρημα: Αν η f είναι συνεχής στο x και f(x)>0 τότε υπάρχει γειτονιά του x στην οποία η f είναι θετική (>0).

Ορισμός: Έστω S ένα υποσύνολο του Rⁿ. Το xRⁿ θα λέγεται σημείο επαφής του S αν για κάθε ε>0 το σύνολο B(x, ε)S είναι μη κενό. Το S θα λέγεται κλειστό αν περιέχει όλα τα σημεία επαφής του. Το S θα λέγεται φραγμένο αν υπάρχει R>0 τ.ω. SB(0, R).

Παράδειγμα: Έστω S = {(x, y): x² + y² <1}. Tα (1, 0), (0, 0) είναι σημεία επαφής του S. Το σύνολο Α = {(x, y): x² + y² £ 1} είναι κλειστό και φραγμένο.

Θεώρημα: Αν η f είναι συνεχής σε κάθε σημείο ενός συνόλου S το οποίο είναι κλειστό και φραγμένο τότε υπάρχει xS με

Ασκήσεις

1. Να εξετάσετε αν υπάρχει η οριακή τιμή των παρακάτω συναρτήσεων στο

    σημείο (0, 0).

    [Yπόδειξη] [Λύση]

2. Να εξετάσετε την συνέχεια των παρακάτω συναρτήσεων στο (0, 0).

    [Λύση]

3. Mπορούμε να ορίσουμε κατάλληλα την συνάρτηση f(x, y) = [sin(x+y)]/3(x+y) στο (0, 0) ώστε να γίνει συνεχής;

   [Υπόδειξη] [Λύση]

4. Έστω ότι οι συναρτήσεις f, g είναι ορισμένες στο ανοικτό σύνολο U.

    Aν για κάποιο a στο U το όριο

    [Υπόδειξη] [Λύση]

[Περιεχόμενα]