Έστω U ένα ανοικτό υποσύνολο στο R², Ρ = (p₁, p₂) ένα σημείο του U και f μια συνάρτηση στο U. Υποθέτουμε ότι η f έχει τοπικό ακρότατο στο P=(p₁, p₂). Τότε επειδή

από τον τύπο του Taylor παίρνουμε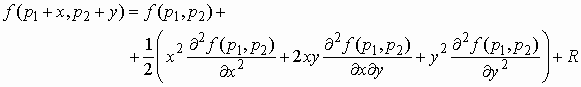

Μπορούμε να αποδείξουμε ότι επειδή στο R εμφανίζονται δυνάμεις των h, k μεγαλύτερες του 2 η συνεισφορά του R στο παραπάνω άθροισμα "κοντά" στο Ρ δεν επηρεάζει το πρόσημο της τετραγωνικής μορφής

Παρατηρούμε ότι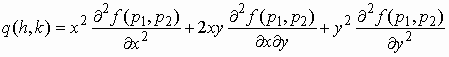 η f έχει τοπικό ελάχιστο (μέγιστο, σαγματικό) στο Ρ αν και μόνο αν το q έχει ελάχιστο (μέγιστο, σαγματικό αντίστοιχα) στο (0, 0).

Αρκεί λοιπόν να μελετήσουμε την συμπεριφορά της q στο (0, 0).

Η γενική μορφή της q είναι η q(x, y)=ax² + bxy + cy² . Ας υποθέσουμε ότι a > 0.

Μετά από πράξεις έχουμε

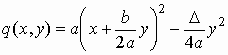
με Δ = b² - 4ac, και η προφανής αντικατάσταση δίνει

Παρατηρούμε ότι για την q ισχύουν τα παρακάτω στο (0, 0)

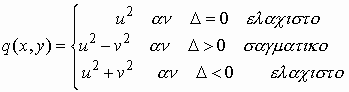
Έτσι αν α > 0

1. Το Ρ είναι τοπικό ελάχιστο της f αν Δ = 0

2. Το Ρ είναι σαγματικό της f αν Δ > 0

3. Το Ρ είναι τοπικό ελάχιστο της f αν Δ < 0

και αν a < 0 το τοπικό ελάχιστο στις παραπάνω περιπτώσεις γίνεται τοπικό μέγιστο.

Αν a = 0 τότε εξετάζουμε το c.

1. Να χαρακτηρίσετε την φύση του σημείου (0, 0) για τις τετραγωνικές μορφές

                2x² + 2xy + y², -4x² + 2xy - y², x² + 2xy + y² [Λύση]

2. Nα χαρακτηρίσετε τα κρίσιμα σημεία της συνάρτησης f(x, y) = x²y + y² + x. [Λύση]

3. Nα ευρεθεί το πλησιέστερο στην αρχή σημείο του επιπέδου 2x + y – z = 1. [Υπόδειξη] [Λύση]

4. Έστω f : [a, b] ® R μια συνάρτηση τ.ω. f''(x)>0 για κάθε x στο [a, b]. Nα αποδείξετε ότι η f δεν έχει σημείο μεγίστου στο (a, b). [Υπόδειξη] [Λύση]

5. Έστω Δ ο μοναδιαίος δίσκος {(x, y): x² + y² £ 1} και f : Δ ® R μια συνάρτηση τ.ω.

σε κάθε σημείο του εσωτερικού του Δ. Να αποδειχθεί ότι η f έχει ακρότατα μόνο στο σύνορο του Δ. [Υπόδειξη] [Λύση]

[Περιεχόμενα]