Έστω η διαφορική εξίσωση πρώτης τάξης

, (1)

όπου οι συναρτήσεις και ορίζονται και έχουν συνεχείς πρώτες μερικές παραγώγους σ’ ένα ανοιχτό και απλά συνεκτικό χωρίο .

Oρισμός: Μια συνάρτηση που έχει συνεχείς πρώτες μερικές παραγώγους στο λέγεται πολλαπλασιαστής Euler ή ολοκληρώνων παράγων για την (1) αν η εξίσωση

, (2)

* Η έννοια του ολοκληρώνοντος παράγοντος εισήχθη από τον Ελβετό μαθηματικό Leonhard Euler (1707-1783) το 1734.

Παρατήρηση: Αν για κάθε , τότε οι εξισώσεις (1) και (2) είναι ισοδύναμες, δηλ. έχουν το ίδιο σύνολο λύσεων.

Εύρεση του πολλαπλασιαστή Euler: Ο ολοκληρώνων παράγων είναι λύση της διαφορικής εξίσωσης με μερικές παραγώγους

,

. (3)

Αν και η επίλυση της μερικής διαφορικής εξίσωσης (3) είναι, γενικά, πολύ δύσκολη μερικές φορές μπορούμε να επιτύχουμε τον προσδιορισμό μιας ειδικής κατηγορίας λύσεων όπως στις παρακάτω περιπτώσεις:

Έστω ότι η συνάρτηση

εξαρτάται μόνο από τη μεταβλητή . Τότε υπάρχει πολλαπλασιαστής Euler που επίσης εξαρτάται μόνο από το και ο οποίος ικανοποιεί τη συνήθη διαφορική εξίσωση (χωριζόμενων μεταβλητών)

. (4)

Έστω ότι η συνάρτηση

εξαρτάται μόνο από τη μεταβλητή . Τότε υπάρχει πολλαπλασιαστής Euler που επίσης εξαρτάται μόνο από το και ο οποίος ικανοποιεί τη συνήθη διαφορική εξίσωση (χωριζόμενων μεταβλητών)

. (5)

[Επιστροφή στα Περιεχόμενα]

ΑΣΚΗΣΕΙΣ:

1. [Λύση]

2. [Λύση]

3. Έστω συνάρτηση η οποία ορίζεται και είναι συνεχώς διαφορίσιμη σ’ ένα ανοιχτό και απλά συνεκτικό χωρίο. Δείξτε ότι αν η ποσότητα

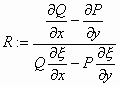
είναι συνάρτηση μόνο της μεταβλητής τότε η διαφορική εξίσωση (1) δέχεται ολοκληρωτικό παράγοντα της μορφής και βρείτε τη γενική μορφή της συνάρτησης . [Λύση]

,

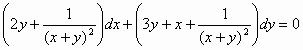αν είναι γνωστό ότι δέχεται πολλαπλασιαστή Euler της μορφής . [Λύση]

,

αν είναι γνωστό ότι δέχεται πολλαπλασιαστή Euler της μορφής .

[Λύση]

[Επιστροφή στα Περιεχόμενα]