Ορισμός: Μια Σ.Δ.Ε. πρώτης τάξης λέγεται ότι είναι χωριζόμενων μεταβλητών όταν μπορεί να πάρει τη μορφή

. (1)

Παρατήρηση: Κάθε εξίσωση χωριζόμενων μεταβλητών είναι ακριβής αφού ισχύει τετριμμένα ότι

.

Μέθοδος επίλυσης: Το γενικό ολοκλήρωμα της (1) δίνεται άμεσα από την σχέση

, (2)

όπου μια αυθαίρετη πραγματική σταθερά. Στην περίπτωση που η εξίσωση (1) συνοδεύεται από την αρχική συνθήκη

, (3)

η λύση δίνεται σε πεπλεγμένη μορφή από τον τύπο

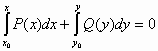. (4)

Γενικά πάντως, ο τύπος (4) είναι ενδεχόμενο να μην προσδιορίζει μοναδικά τη λύση του προβλήματος αρχικών τιμών (1), (3) [δηλ. η (4) μπορεί να έχει πολλές λύσεις ως προς , εκ των οποίων μόνο μια να ικανοποιεί ταυτόχρονα τις (1) και (3)].

[Επιστροφή στα Περιεχόμενα]

ΑΣΚΗΣΕΙΣ:

Να λυθούν οι διαφορικές εξισώσεις:

1. [Λύση]

2. [Λύση]

Να λυθεί το πρόβλημα αρχικών τιμών και να προσδιοριστεί το μέγιστο διάστημα στο οποίο ορίζεται η λύση:

3. , [Λύση]

4. , [Λύση]

[Επιστροφή στα Περιεχόμενα]