ΘΕΩΡΗΜΑΤΑ ΥΠΑΡΞΗΣ ΚΑΙ
ΜΟΝΑΔΙΚΟΤΗΤΑΣ
ΤΗΣ ΛΥΣΗΣ
Έστω 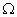 ένα ανοικτό υποσύνολο του
ένα ανοικτό υποσύνολο του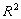 .
.
Ορισμός 1
: Θα λέμε
ότι μια συνάρτηση 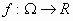 ικανοποιεί μια συνθήκη Lipschitz
ως προς
ικανοποιεί μια συνθήκη Lipschitz
ως προς 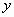 ,
όταν υπάρχει σταθερά
,
όταν υπάρχει σταθερά 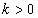 έτσι ώστε για κάθε
έτσι ώστε για κάθε 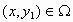 ,
,
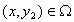 να
ισχύει
να
ισχύει
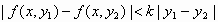 . (*)
. (*)
Σημείωση
: Η κλάση
των συναρτήσεων που ικανοποιούν τη συνθήκη
(*) εισήχθη το 1876 από το Γερμανό μαθηματικό Rudolf
Lipschitz (1832 – 1903) και η σταθερά 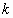 ονομάζεται σταθερά του Lipschitz.
ονομάζεται σταθερά του Lipschitz.
Μια μεγάλη κατηγορία τέτοιων συναρτήσεων
δίνεται από την ακόλουθη:
Πρόταση:
Έστω 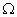 ανοικτό και κυρτό υποσύνολο
του
ανοικτό και κυρτό υποσύνολο
του 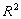 και
συνάρτηση
και
συνάρτηση 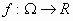 συνεχής.
Αν υπάρχει η
συνεχής.
Αν υπάρχει η 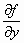 στο
στο
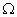 και
είναι φραγμένη, με φράγμα
και
είναι φραγμένη, με φράγμα 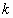 ,
τότε η
,
τότε η 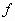 ικανοποιεί τη συνθήκη Lipschitz
ως προς
ικανοποιεί τη συνθήκη Lipschitz
ως προς 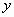 με σταθερά
με σταθερά 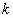 .
.
Θεωρούμε τώρα το πρόβλημα αρχικών τιμών
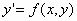 , (1)
, (1)
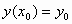 , (2)
, (2)
με
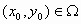 . Έστω
επίσης ορθογώνιο
. Έστω
επίσης ορθογώνιο 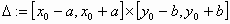 το οποίο είναι υποσύνολο
του
το οποίο είναι υποσύνολο
του 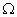 και
έχει κέντρο το σημείο
και
έχει κέντρο το σημείο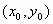 .
.
Θεώρημα 1. (Ύπαρξη λύσης --
(E. Picard - E.
Lindelof) )
Αν η συνάρτηση
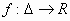 είναι συνεχής και
ικανοποιεί μια συνθήκη Lipschitz ως
προς
είναι συνεχής και
ικανοποιεί μια συνθήκη Lipschitz ως
προς 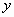 στο
στο
 τότε
υπάρχει διαφορίσιμη συνάρτηση
τότε
υπάρχει διαφορίσιμη συνάρτηση 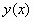 η
οποία είναι λύση του προβλήματος αρχικών
τιμών (1), (2), ορισμένη σ’ ένα διάστημα
η
οποία είναι λύση του προβλήματος αρχικών
τιμών (1), (2), ορισμένη σ’ ένα διάστημα 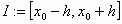 ,
όπου
,
όπου 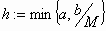 και
και 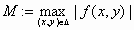 .
.
Σημείωση
: Το
εξαιρετικά σημαντικό αυτό θεώρημα
αποδείχθηκε το 1890 από τον Γάλλο μαθηματικό Emile
Picard (1856 – 1941) και παράλληλα,
αλλά ανεξάρτητα, από τον Φιλανδό μαθηματικό
Ernst Lindelof (1870 – 1946).
Θεώρημα 2. (Μοναδικότητα
της λύσης)
Έστω ότι η συνάρτηση
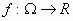 είναι συνεχής και
ικανοποιεί μια συνθήκη Lipschitz ως
προς
είναι συνεχής και
ικανοποιεί μια συνθήκη Lipschitz ως
προς 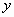 στο
ανοικτό σύνολο
στο
ανοικτό σύνολο 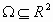 με
με
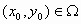 . Αν
. Αν
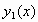 και
και
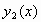 είναι
δύο λύσεις του προβλήματος αρχικών τιμών (1),
(2), ορισμένες στα διαστήματα
είναι
δύο λύσεις του προβλήματος αρχικών τιμών (1),
(2), ορισμένες στα διαστήματα 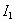 και
και 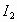 αντίστοιχα, τότε
αντίστοιχα, τότε
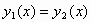 ,
, 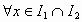 .
(3)
.
(3)
Θεώρημα 3. (Ύπαρξης, μοναδικότητας
και μέγιστου διαστήματος
ορισμού της λύσης)
Αν η συνάρτηση
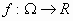 είναι συνεχής και
ικανοποιεί μια συνθήκη Lipschitz ως
προς
είναι συνεχής και
ικανοποιεί μια συνθήκη Lipschitz ως
προς 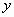 στο
στο
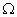 , τότε
υπάρχει μια ακριβώς λύση
, τότε
υπάρχει μια ακριβώς λύση 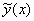 του
προβλήματος αρχικών τιμών (1), (2), η οποία
ορίζεται σε ένα διάστημα
του
προβλήματος αρχικών τιμών (1), (2), η οποία
ορίζεται σε ένα διάστημα 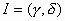 τέτοιο
ώστε κάθε άλλη λύση του προβλήματος να
είναι απλώς ένας περιορισμός της
τέτοιο
ώστε κάθε άλλη λύση του προβλήματος να
είναι απλώς ένας περιορισμός της 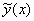 σε
κάποιο υποδιάστημα του
σε
κάποιο υποδιάστημα του 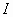 .
Αν επιπλέον το σύνολο
.
Αν επιπλέον το σύνολο 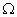 είναι φραγμένο και
είναι φραγμένο και 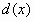 είναι
η απόσταση του σημείου
είναι
η απόσταση του σημείου 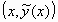 του γραφήματος της
του γραφήματος της 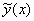 από
το σύνορο
από
το σύνορο 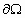 τότε
ισχύει ότι
τότε
ισχύει ότι
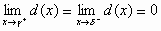 .
.
Θεώρημα 4. (Ύπαρξη
λύσης -- (G. Peano) )
Αν η συνάρτηση
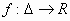 είναι συνεχής στο ορθογώνιο
είναι συνεχής στο ορθογώνιο
 τότε
το πρόβλημα αρχικών τιμών (1), (2), έχει
τουλάχιστον μια λύση ορισμένη στο διάστημα
τότε
το πρόβλημα αρχικών τιμών (1), (2), έχει
τουλάχιστον μια λύση ορισμένη στο διάστημα 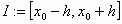 ,
όπου
,
όπου 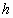 είναι όπως στο θεώρημα Picard
– Lindelof.
είναι όπως στο θεώρημα Picard
– Lindelof.
Σημείωση
: Το θεώρημα
αυτό αποδείχθηκε το1886 από τον Ιταλό
μαθηματικό Giuseppe Peano (1858 – 1932). Συγκρίνοντάς
το με το θεώρημα Picard – Lindelof, παρατηρούμε
ότι και μόνο η υπόθεση της συνέχειας της 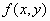 αρκεί για την ύπαρξη μιας
τουλάχιστον λύσης του προβλήματος αρχικών
τιμών (1), (2). Απλά παραδείγματα όμως δείχνουν
ότι αν η
αρκεί για την ύπαρξη μιας
τουλάχιστον λύσης του προβλήματος αρχικών
τιμών (1), (2). Απλά παραδείγματα όμως δείχνουν
ότι αν η 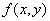 δεν
ικανοποιεί επίσης μια συνθήκη Lipschitz ως προς
δεν
ικανοποιεί επίσης μια συνθήκη Lipschitz ως προς 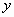 τότε η λύση αυτή δεν είναι η
μοναδική !
τότε η λύση αυτή δεν είναι η
μοναδική !
[Επιστροφή
στα Περιεχόμενα]
ΑΣΚΗΣΕΙΣ
:
Δείξτε ότι τα ακόλουθα
προβλήματα αρχικών τιμών έχουν μοναδική
λύση:
1. 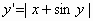 ,
, 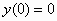 .
[Λύση]
.
[Λύση]
2. 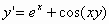 ,
, 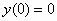 .
[Λύση]
.
[Λύση]
3. 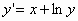 ,
, 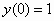 .
[Λύση]
.
[Λύση]
4. Πως εξηγείτε το γεγονός ότι το
πρόβλημα αρχικών τιμών
:
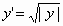 ,
, 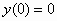 ,
,
δέχεται ως λύσεις
τις διαφορετικές
συναρτήσεις
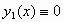 και
και
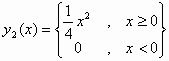 .
.
[Λύση]
[
Επιστροφή
στα Περιεχόμενα]
![]() ένα ανοικτό υποσύνολο του
ένα ανοικτό υποσύνολο του![]() .
.![]() . (*)
. (*)![]() , (1)
, (1)![]() , (2)
, (2)![]() ,
, ![]() .
(3)
.
(3)![]() .
.![]() ,
, ![]() .
[Λύση]
.
[Λύση]![]() ,
, ![]() .
[Λύση]
.
[Λύση]![]() ,
, ![]() .
[Λύση]
.
[Λύση]![]() ,
, ![]() ,
,![]() και
και
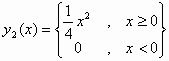 .
.