Τυχαίες Μεταβλητές

 

Τυχαία μεταβλητή ονομάζεται μία μετρήσιμη συνάρτηση που αντιστοιχεί σε κάθε στοιχειώδες συμβάν ωΩ έναν αριθμό Χ(ω).

Συνάρτηση κατανομής της τυχαίας μεταβλητής Χ ονομάζεται η συνάρτηση F(x)=P[Xx]. Επομένως P[x1<X x2]= F(x2)- F(x1).

Διακριτή ονομάζεται η τυχαία μεταβλητή που σε κάθε ωΩ αντιστοιχεί μία τιμή από ένα διακριτό (πεπερασμένο ή αριθμήσιμο) σύνολο { x1, x2,…, xn}.

Έστω Pi P[X=xi] η πιθανότητα να πάρει η Χ την τιμή xi.

Διωνυμική κατανομή:

Κατανομή Poisson:

Γεωμετρική κατανομή: ,όπου q=1-p.

 

Συνεχής ονομάζεται η τυχαία μεταβλητή Χ, που έχει συνάρτηση κατανομής F(x) στη μορφή . Η συνάρτηση f(y) ονομάζεται πυκνότητα κατανομής της τυχαίας μεταβλητής Χ. Iσχύει: f(x)=F’(x).

Ομοιόμορφη κατανομή:

 

 

Eκθετική κατανομή:

 

 

Κανονική κατανομή:

 

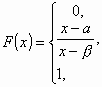
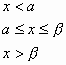
Κατανομή Weibull:

 

 

Κατανομή Γάμα:

 

Έστω g μετρήσιμη συνάρτηση και Χ τυχαία μεταβλητή. Η Y= g(X) ονομάζεται συνάρτηση της τυχαίας μεταβλητής Χ. Εάν η g(x) είναι μονότονη και αύξουσα τότε :

FY(x)= FX(g-1(x)).

Εάν η g-1(x) παραγωγίζεται τότε: fY(x)= (g-1(x))΄· fX(g-1(x)).

 

Ασκήσεις

Άσκηση 39

Δύο παίχτες στρίβουν ένα νόμισμα και εάν πέσει «γράμματα» τότε ο πρώτος παίκτης δίνει 1 δραχμή στο δεύτερο, ενώ εάν πέσει «Κορώνα» τότε ο δεύτερος παίκτης δίνε στον πρώτο 2 δραχμές. Ορίστε την τυχαία μεταβλητή Χ που δίνει το κέρδος του πρώτου παίκτη μετά από το στρίψιμο του νομίσματος.

Λύση άσκησης

 

Άσκηση 40

Στο σχήμα Bernoulli με πιθανότητα επιτυχίας p ορίστε τυχαία μεταβλητή Μ ίση με το πλήθος επιτυχιών σε n επαναλήψεις.

Λύση άσκησης

 

Άσκηση 41

Στο διάστημα [0, 1] σε συμφωνία με την αρχή της γεωμετρικής πιθανότητας πέφτει τυχαία ιδανικό σημείο. Δείξτε ότι είναι τυχαία μεταβλητή το ίδιο το σημείο του διαστήματος.

Υπόδειξη άσκησης

Λύση άσκησης

 

Άσκηση 42

Σε διαγώνισμα καλείται ένας φοιτητής να λύσει n= 4 προβλήματα. Η πιθανότητα να λύσει σωστά κάθε πρόβλημα είναι p= 0.8. Βρείτε την κατανομή της τυχαίας μεταβλητής Μ, που ισούται με τον αριθμό των προβλημάτων που λύθηκαν σωστά από το φοιτητή.

Υπόδειξη άσκησης

Λύση άσκησης

 

Άσκηση 43

Σε ένα φυσικό πείραμα εμφανίζεται κάποιο φαινόμενο με πιθανότητα p= 0.4. έστω Χ τυχαία μεταβλητή που δείχνει τον αριθμό των «άτυχων» πειραμάτων που κάνει ο πειραματιστής μέχρι να πάρει το ζητούμενο φαινόμενο. Βρείτε την κατανομή της Χ και δώστε την γραφική παράσταση της συνάρτησης κατανομής F(x).

Υπόδειξη άσκησης

Λύση άσκησης

 

Άσκηση 44

Δώστε την κατανομή της τυχαίας μεταβλητής Χ, που δίνει τον αριθμό των τυχερών νούμερων σε ένα τυχαίο δελτίο ΛΟΤΟ.

Λύση άσκησης

 

Άσκηση 45

Στο παιχνίδι ΛΟΤΟ το 6άρι κερδίζει 5.000.000 δρχ. το 5άρι 30.000 και το 4άρι 20.000 δρχ. Βρείτε την κατανομή της τυχαίας μεταβλητής Υ που δηλώνει τα κέρδη ενός παίκτη του ΛΟΤΟ, όταν η συμμετοχή κοστίζει 100 δρχ.

Υπόδειξη άσκησης

Λύση άσκησης

 

Άσκηση 46

Έστω X τυχαία μεταβλητή που ακολουθεί την τυποποιημένη κανονική κατανομή. Βρείτε την κατανομή της τυχαίας μεταβλητής Υ=Χ2.

Υπόδειξη άσκησης

Λύση άσκησης

 

Άσκηση 47

Έστω f(x) η πυκνότητα κατανομής της τυχαίας μεταβλητής Χ, και f(x)>0 για κάθε x. βρείτε την κατανομή της τυχαίας μεταβλητής Υ=F(X), όπου F(X) η συνάρτηση κατανομής της Χ.

Λύση άσκησης

 

Άσκηση 48

Έστω Χ μια τυχαία μεταβλητή που ακολουθεί την κανονική κατανομή με μέση τιμή m και διασπορά σ2. Βρείτε την κατανομή της Υ= eX που ονομάζεται λογαριθμοκανονική.

Λύση άσκησης

 

Άσκηση 49

Έστω X θετική τυχαία μεταβλητή που ακολουθεί την εκθετική κατανομή με παράμετρο λ= (κατανομή x2 με δύο βαθμούς ελευθερίας). Βρείτε την κατανομή της .

Υπόδειξη άσκησης

Λύση άσκησης

 

Άσκηση 50

Έστω Χ τυχαία μεταβλητή που ακολουθεί την τυποποιημένη κανονική κατανομή. Βρείτε την κατανομή της Υ= σΧ+ m με σ>0.

Υπόδειξη άσκησης

Λύση άσκησης

 

Περιεχόμενα