Διανύσματικός Λογισμός

Στον συνηθισμένο χώρο δύο ευθύγραμμα τμήματα λέγονται ισοδύναμα αν έχουν α) την ίδια διεύθυνση, β) την ίδια φορά και γ) το ίδιο μήκος.

Ισοδύναμα ευθύγραμμα τμήματα ορίζουν το ίδιο (ελεύθερο) διάνυσμα. Το σύνολο των διανυσμάτων είναι γραμμικός χώρος.

Αν $\vec{a}\,$,$\vec{b}\,$ είναι διανύσματα τότε |$\vec{a}\,$| συμβολίζει το μήκος του $\vec{a}\,$ και $\angle$($\vec{a}\,$,$\vec{b}\,$) την μικρότερη προσημασμένη γωνία που πρέπει να περιστραφεί το $\vec{a}\,$ για να συμπέσει με το $\vec{b}\,$, όταν θεωρηθούν να έχουν κοινή αρχή και η περιστροφή γίνεται στο επίπεδο που ορίζουν. Θετική είναι η περιστροφή που είναι αντίθετη της περιστροφής των δεικτών ενός ρολογιού.

Μιά διατεταγμένη βάση ($\vec{a}\,$,$\vec{b}\,$,$\vec{c}\,$) του γραμμικού χώρου πού ορίσαμε λέγεται σύστημα αναφοράς.

Το εσωτερικό γινόμενο δύο διανυσμάτων ορίζεται ως

$$\vec{a}\, \vec{b}\, \vec{a}\, \vec{b}\, \angle \vec{a}\, \vec{b}\,$$ (1)

Το εξωτερικό ή διανυσματικό γινόμενο δύο διανυσμάτων $\vec{a}\,$,$\vec{b}\,$ είναι ένα τρίτο διάνυσμα $\vec{c}\,$, που έχει διεύθυνση κάθετη προς το επίπεδο των $\vec{a}\,$,$\vec{b}\,$, φορά τέτοια ώστε το σύστημα αναφοράς ($\vec{a}\,$,$\vec{b}\,$,$\vec{c}\,$) να είναι δεξιόστροφο και μέτρο

$$\vec{c}\, \vec{a}\, \vec{b}\, \angle \vec{a}\, \vec{b}\,$$ (2)

Το εξωτερικό γινόμενο των διανυσμάτων $\vec{a}\,$,$\vec{b}\,$ συμβολίζεται $\vec{a}\,$ x $\vec{b}\,$. Το μέτρο του $\vec{a}\,$ x $\vec{b}\,$ είναι ίσο προς το εμβαδόν του παραλληλογράμμου με πλευρές $\vec{a}\,$,$\vec{b}\,$.

Το μικτό γινόμενο τριών διανυσμάτων $\vec{a}\,$, $\vec{b}\,$ και $\vec{c}\,$ είναι

$$\vec{a}\, \vec{b}\, \vec{c}\, \vec{a}\, \vec{b}\, \vec{c}\,$$ (3)

Το μικτό γινόμενο δίνει τον (προσημασμένο) όγκο του παραλληλεπιπέδου που ορίζουν τα διανύσματα $\vec{a}\,$, $\vec{b}\,$ και $\vec{c}\,$.

Για το δις εξωτερικό γινόμενο έχουμε

$$\vec{a}\, \vec{b}\, \vec{c}\, \vec{a}\, \vec{c}\, \vec{b}\, \vec{a}\, \vec{b}\, \vec{c}\,$$ (4)

Αν ($\alpha_{1}^{}$,$\alpha_{2}^{}$,$\alpha_{3}^{}$), ($\beta_{1}^{}$,$\beta_{2}^{}$,$\beta_{3}^{}$) και ($\gamma_{1}^{}$,$\gamma_{2}^{}$,$\gamma_{3}^{}$) oι συντεταγμένες των δια/-νυσ/-μάτων $\vec{a}\,$, $\vec{b}\,$ και $\vec{c}\,$ αντίστοιχα ως προς ορθοκανονικό σύστημα συντεταγμένων ($\vec{x}_{0}^{}$,$\vec{y}_{0}^{}$,$\vec{z}_{0}^{}$), τότε έχουμε

$$\vec{a}\, \vec{b}\, \alpha_{1}^{} \beta_{1}^{} \alpha_{2}^{} \beta_{2}^{} \alpha_{3}^{} \beta_{3}^{}$$ (5)

και

$$\vec{a}\, \vec{b}\, \left\vert\vphantom{\begin{array}{ccc} \vec{x}_0 & \vec{y}_0 & \v... ...pha_1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \end{array}}\right. \begin{array}{ccc} \vec{x}_0 & \vec{y}_0 & \vec{z}_0 \\ \alpha_1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \end{array} \left.\vphantom{\begin{array}{ccc} \vec{x}_0 & \vec{y}_0 & \vec{z... ...1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \end{array}}\right\vert \vec{a}\, \vec{b}\, \vec{c}\, \left\vert\vphantom{\begin{array}{ccc} \alpha_1 & \alpha_2 & \alp... ...ta_1 & \beta_2 & \beta_3 \\ \gamma_1 & \gamma_2 & \gamma_3 \end{array}}\right. \begin{array}{ccc} \alpha_1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \\ \gamma_1 & \gamma_2 & \gamma_3 \end{array} \left.\vphantom{\begin{array}{ccc} \alpha_1 & \alpha_2 & \alpha_3... ... 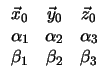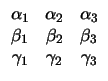& \beta_2 & \beta_3 \\ \gamma_1 & \gamma_2 & \gamma_3 \end{array}}\right\vert$$ (6)