

Next: Άσκηση
Up: No Title
Previous: Λύση
Η παραμετρική εξίσωση ενός επιπέδου παράλληλου προς δύο μη-συγγραμμικά διανύσματα
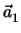 ,
, 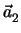 που περνάει από ένα σημείο P1 με διάνυσμα θέσης
που περνάει από ένα σημείο P1 με διάνυσμα θέσης 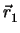 είναι
είναι
Το επίπεδο που περνάει από το P1 και είναι κάθετο στο διάνυσμα
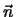 δίνεται από την εξίσωση
δίνεται από την εξίσωση
Σε συντεταγμένες η εξίσωση του επιπέδου είναι
Ax + By + Cz + D = 0, με (A, B, C) 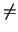 (0, 0, 0).
(0, 0, 0). |
|
|
(28) |
Προφανώς το διάνυσμα
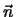 = (A, B, C) είναι κάθετο στο έν λόγω
επίπεδο.
= (A, B, C) είναι κάθετο στο έν λόγω
επίπεδο.
Δύο μη-παράλληλα επίπεδα ορίζουν μια ευθεία στο χώρο. H
ευθεία που περνάει από το σημείο P1 και είναι παράλληλη στo
διάνυσμα
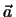 = (
= (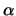 ,
,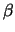 ,
,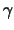 ) είναι
) είναι
Δύο επίπεδα
Aix + Biy + Ciz + Di = 0, i = 1, 2 είναι παράλληλα,
αν
ενώ συμπίπτουν, αν
Για την σχετική θέση τριών επιπέδων
Aix + Biy + Ciz + Di = 0, i = 1, 2, 3
σημαντικό ρόλο παίζουν οι τάξεις
r(A), r(B) των πινάκων
Έχουμε τις εξής περιπτώσεις:
(α)
r(A) = r(B) = 1, τα τρία επίπεδα συμπίπτουν,
(β)
r(A) = 1, r(B) = 2, τα τρία επίπεδα είναι παράλληλα,
(γ)
r(A) = r(B) = 2, τα τρία επίπεδα διέρχονται από την ίδια
ευθεία,
(δ)
r(A) = 2, r(B) = 3, τα τρία επίπεδα είναι παράλληλα προς μία
ευθεία, αλλά δεν είναι παράλληλα μεταξύ τους, ούτε διέρχονται από
την ίδια ευθεία,
(ε)
r(A) = r(B) = 3, τα επίπεδα έχουν κοινό ένα μόνο σημείο.
Δύο επίπεδα
Aix + Biy + Ciz + Di = 0, i = 1, 2 ορίζουν μιά αξονική δέσμη επιπέδων που δίνεται από την εξίσωση
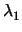 (A1x + B1y + C1z + D1) + (A1x + B1y + C1z + D1) + 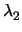 (A2x + B2y + C2z + D2) = 0. (A2x + B2y + C2z + D2) = 0. |
|
|
(33) |
Τρία επίπεδα
Aix + Biy + Ciz + Di = 0, i = 1, 2, 3 που περνούν από
ένα σημείο ορίζουν μιά κεντρική δέσμη επιπέδων με εξίσωση
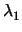 (A1x + B1y + C1z + D1) + (A1x + B1y + C1z + D1) + 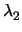 (A2x + B2y + C2z + D2) (A2x + B2y + C2z + D2) |
|
|
|
+ 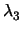 (A3x + B3y + C3z + D3) (A3x + B3y + C3z + D3) |
= |
0. |
(34) |
Η απόσταση ενός σημείου
P0(x0, y0, z0) από ένα επίπεδο
Ax + By + Cz + D = 0 δίνεται από την εξίσωση
d = 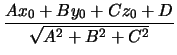 . . |
|
|
(35) |
Η απόσταση ενός σημείου
P0(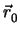 ) από την ευθεία που
περνάει από το σημείο
P1(
) από την ευθεία που
περνάει από το σημείο
P1(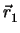 ) και είναι παράλληλη στο
διάνυσμα
) και είναι παράλληλη στο
διάνυσμα 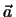 είναι
είναι
d = 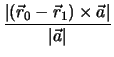 . . |
|
|
(36) |
Δύο ευθείες
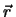 =
= 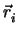 + t
+ t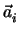 , i = 1, 2 είναι
ασύμβατες αν και μόνο αν
(
, i = 1, 2 είναι
ασύμβατες αν και μόνο αν
(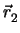 -
- 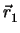 ,
,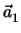 ,
,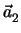 )
) 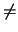 0. Η ελάχιστη απόσταση δύο ασύμβατων ευθειών
είναι
0. Η ελάχιστη απόσταση δύο ασύμβατων ευθειών
είναι
d = 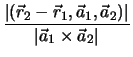 . . |
|
|
(37) |


Next: Άσκηση
Up: No Title
Previous: Λύση
Aristophanes Dimakis
1999-10-05
![]() ,
, ![]() που περνάει από ένα σημείο P1 με διάνυσμα θέσης
που περνάει από ένα σημείο P1 με διάνυσμα θέσης ![]() είναι
είναι
![]() = (
= (![]() ,
,![]() ,
,![]() ) είναι
) είναι
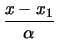 =
= 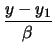 =
= 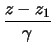 .
.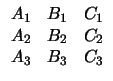
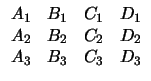
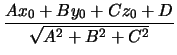 .
.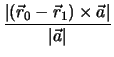 .
.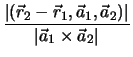 .
.