Δυναμοσειρές

Ορισμός 47   Αν $\{ a_k \}$ είναι μια οποιαδήποτε ακολουθία στο $\mathbb R$, τότε τη σειρά $\sum^\infty _{k=0} a _k$ την ονομάζουμε $\hbox{δυναμοσειρά}$ με συντελεστές $a_k$. Έστω

$$\alpha = \limsup_{k \rightarrow \infty} \sqrt[k]{\vert a_k\vert} .$$

Τότε $0\leq \alpha \leq + \infty$.

Ορισμός 48   Τον αριθμό $R=\frac{1}{\alpha}$ τον ονομάζουμε $\hbox{ακτίνα σύγκλισης}$ της δυναμοσειράς. Δεχόμαστε $\frac{1}{0} = + \infty, \ \frac{1}{+\infty} = 0$. Άρα $0 \leq R \leq +\infty$. Αυτή την ονομασία δικαιολογεί το ακόλουθο:

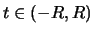
Θεώρημα 49   (α)    Αν $t \in (-R, R)$ η δυναμοσειρά συγκλίνει απολύτως στο $t$.
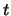
(β)     Αν $t \notin [-R, R]$ η δυναμοσειρά αποκλίνει στο $t$.
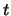
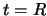
(γ)    Για $t= R$ δεν υπάρχει γενικό συμπέρασμα.
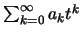
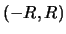
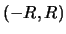
(δ)    Η $\sum ^\infty _{k=0} a_k t^k$ συγκλίνει ομοιόμορφα σε οποιοδήποτε διάστημα $[a, b]$ το οποίο περιέχεται στο $(-R, R)$. Το διάστημα $(-R, R)$ ονομάζεται διάστημα σύγκλισης της δυναμοσειράς.